

| ▲ Mathematics |
Below is a picture of what is called a "prismatic ring" (the term coined by Martin Gardner). The one below is a square prismatic ring - if the ring is cut, the cross-section is a square. To make the shape below, a square is extruded into a long prism, one end is given a twist of 180 degrees w.r.t. the other end, and the ends are joined. It has 2 sides and 2 edges. Other shapes can be formed by giving the bar different numbers of twists.

(This was carved from a wooden curtain ring!)
Much more about prismatic rings can be found in Martin Gardner's book "Fractal Music, Hypercards and More..." 1991/1992 W.H. Freeman & Co, New York, pages 76-87.
I found an interesting correlation between the prismatic rings and Celtic knotwork designs....
Let the number of sides of the cross section of a prismatic ring be n (for the above ring, n=4). Let k be the number of 1/n turns the prism is given before its ends are joined (for the above ring, k=2 since the prism was twisted 180 degrees and there are 4 sides). Let's make a table of the number of faces the resulting prismatic ring has when n & k are known.
0 |
1 |
2 |
3 |
4 |
|
2 |
2 |
1 |
2 |
1 |
2 |
3 |
3 |
1 |
1 |
3 |
1 |
4 |
4 |
1 |
2 |
1 |
4 |
5 |
5 |
1 |
1 |
1 |
1 |
6 |
6 |
1 |
2 |
3 |
2 |
(bold numbers in top row - values of k, bold numbers in left column - values of n)
We find an interesting point; the number of sides is simply the greatest common divisor of k & n. We can tell from this that the prismatic ring will have only 1 side when n & k are relatively prime.
Now, the relation to celtic knotworks. Have a look at the picture below.
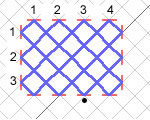
Imagine that the short red bars are mirrors. Imagine we are standing at the mirror denoted by the black dot, and we shine a laser beam in a north-west direction. The beam will bounce round the mirrors until it returns to where we are standing. The blue path denotes the laser beam.
For this particular arrangement of mirrors, the region in which the laser beam travels is 4 mirrors wide and 3 mirrors high (as denoted by the numbers in the figure).
For a 4 x 3 region, there is only one path the laser beam can follow. This is not the case for other sizes of regions. For example, a 6 x 4 region has two possible paths the laser beam can follow. These are shown below.
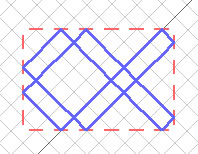
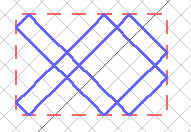
Notice anything? What is the greatest common divisor of 6 & 4? Answer: 2. And we have two separate paths! As it turns out, if we have a region w mirrors wide and h mirrors high, the number of separate paths the beam can travel is the greatest common divisor of w & h.
(The relation to Celtic knotworks: the blue path can be thought of as a ribbon which, at each crossover, can either go over or under the other part of the ribbon. This forms an interlace pattern, which is the basis of many Celtic designs.)
If we make a table of w & h, we see that it is identical to the table for the prismatic rings:
1 |
2 |
3 |
4 |
5 |
|
1 |
1 |
1 |
1 |
1 |
1 |
2 |
1 |
2 |
1 |
2 |
1 |
3 |
1 |
1 |
3 |
1 |
1 |
4 |
1 |
2 |
1 |
4 |
1 |
5 |
1 |
1 |
1 |
1 |
5 |
(bold numbers in top row - values of w, bold numbers in left column - values of h)
Again, whenever w & h are relatively prime, the laser beam can only travel along one path.
I would be interested to know if anyone has though about this connection before, and if it is of any possible use!
| ▲ Mathematics |